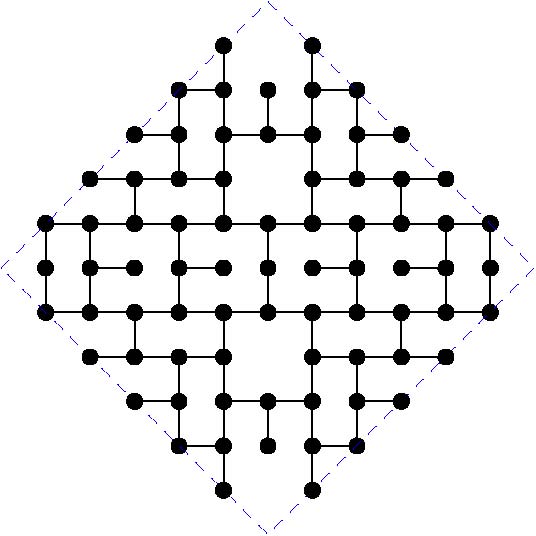
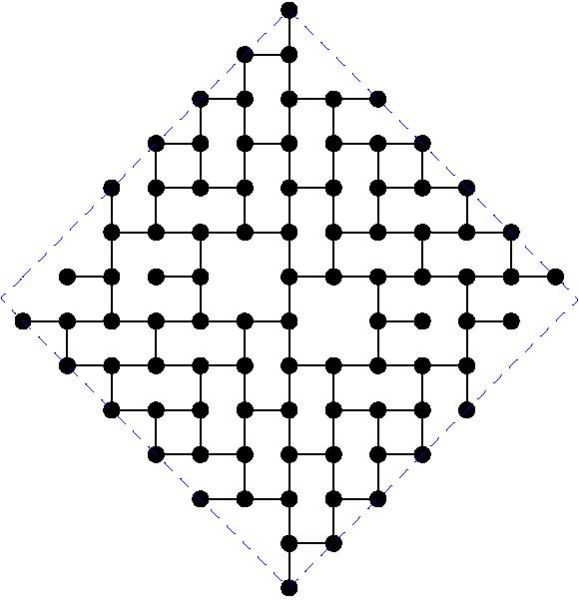
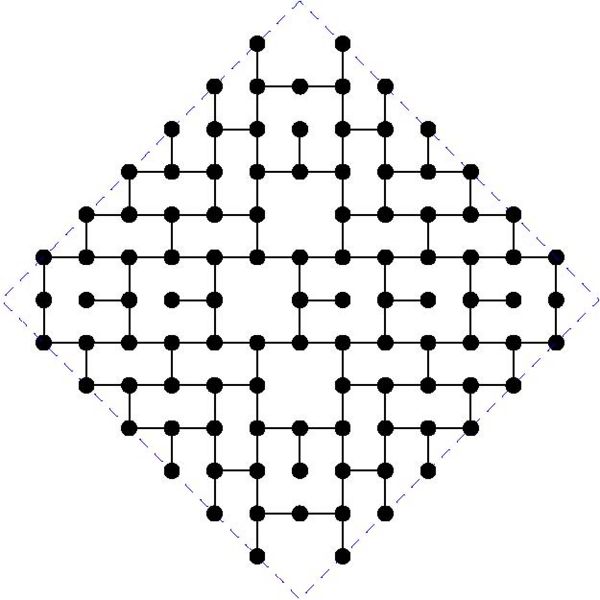
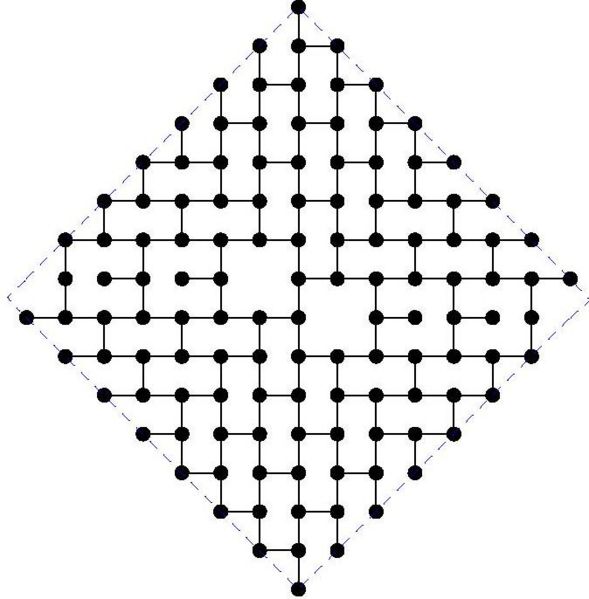
MaxDDBS in the mesh
From Combinatorics Wiki
The mesh as host graph
An important special case is when the host graph G is a common parallel architecture, such as the mesh, the hypercube, the butterfly, etc. The paper by Miller, Perez-Roses, and Ryan (2011) computes upper and lower bounds for the largest subgraph of the mesh in arbitrary dimension. Moreover, it discusses the cases of degree 4 in dimension 3, and degree 3 in dimension 2, where some general constructions are given, that are asymptotically optimal.
Subgraphs of degree 3 in the 2-dimensional mesh
If we take an infinite 2-dimensional mesh as a host graph, then the only case that makes sense is d=3. In this case, the upper bound for the order of the largest subgraph is:
- [math] 2p^2 + 2p +1 [/math], if k is even, and
- [math] 2p^2 + 4p +2 [/math], if k is odd,
where [math] p = \lfloor k/2 \rfloor [/math].
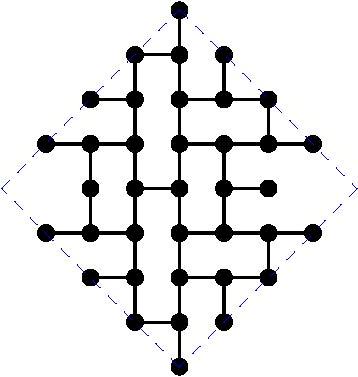
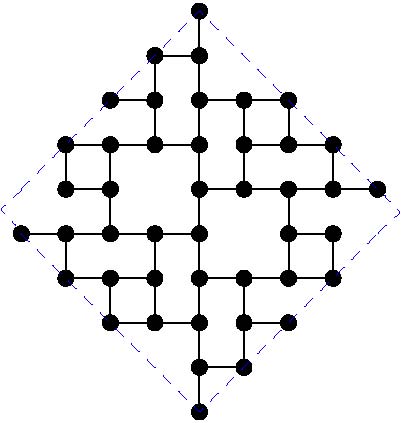
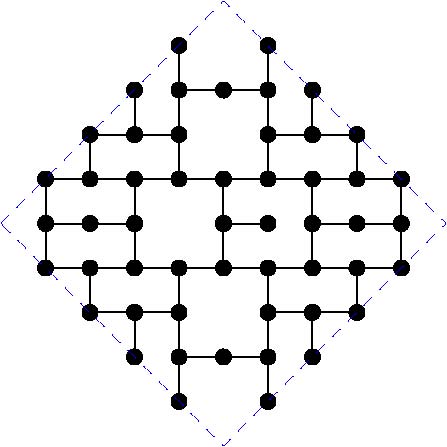
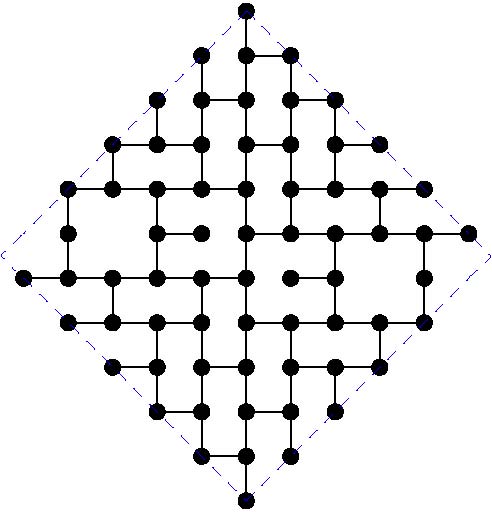
The paper by Miller, Perez-Roses and Ryan (2011) gives general constructions for this case, that come asymptotically close to the upper bounds. However, for particular values of the diameter, the constructions do not provide the largest known subgraphs. Here we maintain a list of the largest known subgraphs of degree 3 for some small values of the diameter k.
The following table gives the order of the largest known subgraphs. If you can beat any of these constructions, please get in contact with the moderator in order to include your graph:
| diameter [math]k[/math] | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| best upper bound | 4 | 6 | 10 | 14 | 22 | 32 | 41 | 50 | 61 | 72 | 85 | 98 | 113 | 128 | 145 |
| order of largest graph | 4 | 6 | 10 | 14 | 22 | 28 | 37 | 44 | 52 | 68 | 77 | 90 | 104 | 124 | 135 |
| percent of upper bound | 100 | 100 | 100 | 100 | 100 | 87.5 | 90.2 | 88 | 85.2 | 94.4 | 90.5 | 91.8 | 92 | 96.8 | 93 |
Next is the table with the color codes:
| Color | Details |
| * | Graphs found by Hebert Perez-Roses, Mirka Miller, and Joe Ryan |
| * | Optimal graphs found by Anthony Dekker by exhaustive search |
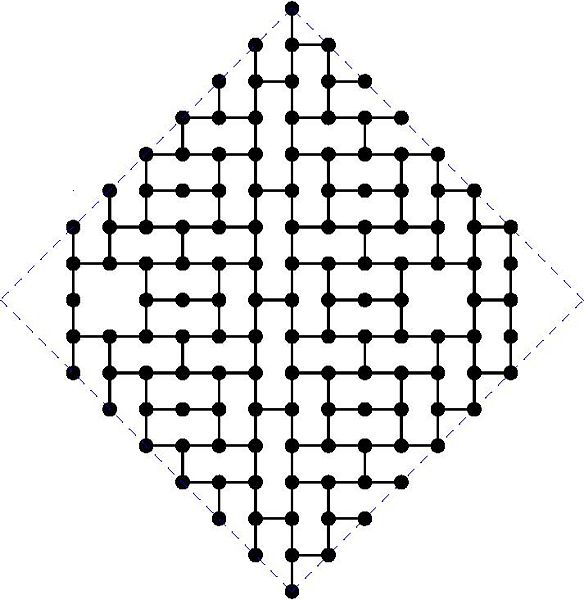
And the actual graphs are shown here:
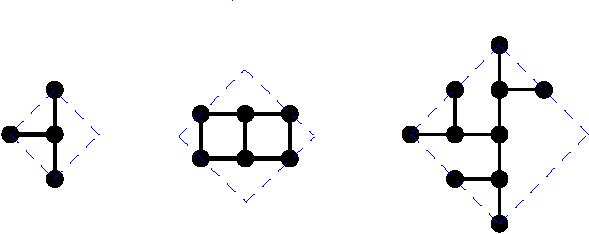
Diameters 2, 3, 4:
Diameter 5:
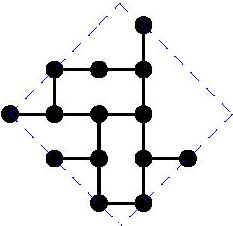
Diameter 6:
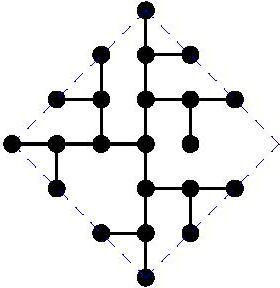
Diameter 7:
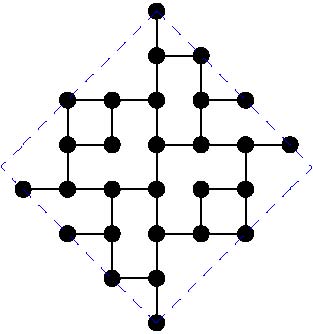
Diameter 8:
Diameter 9:
Diameter 10:
Diameter 11:
Diameter 12:
Diameter 13:
Diameter 14:
Diameter 15:
Diameter 16:
References
- Dekker, Anthony; Perez-Roses, Hebert; Pineda-Villavicencio, Guillermo; Watters, Paul (2011), "The Maximum Degree&Diameter-Bounded Subgraph and its Applications". Journal of Mathematical Modelling and Algorithms. DOI 10.1007/s10852-012-9182-8.
- Miller, Mirka; Perez-Roses, Hebert; Ryan, Joe (2011), "The Maximum Degree&Diameter-Bounded Subgraph in the Mesh", to appear in Discrete Applied Mathematics.